[디지털 통신] CH1. Signals and Spectra

1. Classification of Signals

○ Deterministic vs. Random Signal

    시간을 지정하여 불확실성이 없다 -> Deterministic signal

    불확실성이 있으면 Random Signal이다. 

○ Periodic  vs Non-Periodic Signal

    주기 T마다 신호가 반복되면 periodic signal

○  Analog vs. Discrete Signal

    특정 시간에만 존재하면 discrete, 연속적인 함수이면 analog signal

○  Energy vs Power Signal 

     * Energy Signal

        Finite energy but zero average power 

        deterministic & non-periodic signal일 때 사용함

 

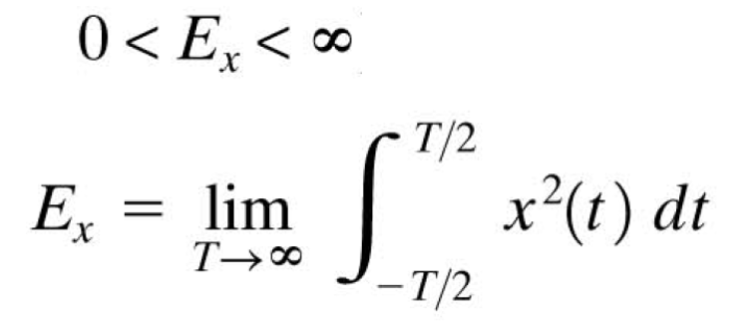
      * Power Signal

        Finite power but infinite energy

        Periodic signal || random signal일 때 사용함

 

Unit Impulse (Dirac Delta) Function 

 

 

2. Spectral Density and Autocorrelation

Spectral Density: 주파수 영역에서 신호의 energy, power의 분포를 나타낸다.

1) Energy Spectral Density (ESD) - Energy Signals

얼마나 Energy Component를 가지고 있는지를 표현한 수식이다. 

2) Power Spectral Density (PSD) 

Coefficient를 가지고 power Spectral density 구하는 방식 & 정석적인 방식 모두 숙지해야 한다.

* Periodic power signals으로 주어질 때 

 

* non-periodic power signals (Random signal)

 

3) Autocorrelation 

자기 자신과 time shift가 일어난 자의 연관성을 살펴볼 때 사용하는 식 

Correlation이 작다 -> 빠르게 변화하는 함수임을 알려준다. 

다른 함수와의 상관관계를 알기 위해서는 cross correlation을 사용한다.

3. Random Signals

1) Random Processes

통신시스템은 random하게 모델이 구성되어 있다. 

noise, interference, Fading 은 대표적인 random processes이다.

2) Random Events 

Random Events는 확률로 표현한다. 

joint probability, Conditional probability, Statistical Independence를 모두 만족한다. 

 

3) Random Variables 

event space에서 실수 대응함수를 random variables이라 한다. 

random variable은 범위가 유한하거나 셀 수 있는 discrete-valued, 범위가 무한하거나 셀 수 없는 Continuous valued으로 표현한다.

 

# Probability Mass Function (pmf)

# Cumulative Density Function (CDF)

 

#Probability Density Function (PDF)

 

-Uniform pdf

 

-Gaussian pdf

 

 

4) Stationarity of Random Processes

    (1) Strict sense Stationary (SSS)

         시간에 영향을 받지 않는 CDF를 가진다.

    (2) Wide sense Stationary (WSS)

         1차 모먼트와 2차 모먼트 값의 변화가 없을 때

 

4. Noise in Communication Systems

 - 원치 않는 신호들이 포함되어 있는 것을 잡음이라고 한다. 

1) Thermal Noise (Additive White Gaussian Noise )

    -thermal motion에 의해 발생한다. 

2) Additive Noise model 

    수신되는 신호는 보낸 신호와 잡음의 합으로 표현된다.

    r(t)= s(t)+n(t)의 형식으로 더해진다. 

 

3) Gaussian Distribution

    시스템 잡음 모델에는 가우시안 분포를 사용한다. 

    Central limit theorem 

N이 충분히 크면 신호와 잡음 모두 가우시안 분포를 따른다. 

4) White Noise  

 잡음이 전체 주파수 대역에서 power spectral Density 가 일정하게 유지되면 백색소음이라 한다.

 두 어떤 white noise도 uncorrelated 되어 있다.